|
Показано, что отвод сопловой части верхней холодной завесы от кромки проема внутрь помещения, т.е. частичное экранирование струи ограждением, позволяет в ряде случаев повысить температуру втекающей смеси и уменьшить тепловую мощность компенсации теплопотерь. 1. Течение в проеме с экранированной верхней струей представлено на рис.1. Экранированная до сечения «а» струя имеет расход воздуха Ga = λaGз с температурой t2, где Gз – расход воздуха через завесу, λa = (0,55/ξ)(a/bзcosα)0,5 – коэффициент эжекции струи в сечении «а», bз – ширина сопла завесы, ξ – коэффициент качества струи [1]. Допустимость плоской постановки задачи обоснована в [1]. На участке до сечения «а» теплопотери экранированной струи отсутствуют. Далее в проеме развивается структура, контактирующая наружной стороной с холодным воздухом (температура t1) и обрастающая холодными эжектированными массами. Однако эти массы не вступают в прямой контакт с ядром постоянного массового расхода струи Gз, поскольку между ними протекают массы, эжектированные на участке «а» с температурой t2. |
Ю. Н. Марр |
Теплые массы с расходом Gэа = 0,5(λa - 1)Gз , перемешиваясь с холодными, продолжают экранировать ядро постоянного расхода струи. Экранируемое ядро охлаждается медленнее. В зависимости от установившегося режима течения часть эжектированных снаружи масс затечет в проем вместе с ядром постоянного расхода и внутренними эжектированными массами. Полные теплопотери защитной структуры будут определяться тремя обстоятельствами: интенсивностью охлаждения ядра постоянного расхода струи, величиной расхода воздуха, отделяющегося и уходящего от струи наружу и величиной расхода наружного воздуха, затекающего в проем.
2. Поскольку экранированная струя развивается в ограниченном пространстве, возникают деформации полей давления и скоростей. Сделаем оценки возможным деформациям (Соображение о необходимости учета влияния ограниченного пространства на развитие струи принадлежит В.Г.Караджи).
Для оценки использовалось решение задачи о распространении свободной струи вблизи экрана [2] (раздел 6, §2, стр.217-229). Рассмотрим завесу с шириной сопла bз = 0,15 м в диапазоне расстояний а = 1 – 3 м, с углом выхода струи 300 к плоскости проема в сторону улицы. Расстояние от экрана (вертикальной стены ограждения) до сопла определяется как с/bз ≥ (а/bз)tgα + 0,5λa2/cosα. В этом выражении ширина струи в сечении «а» вычислялась по среднемассовой скорости. Можно показать, что угол натекания струи на экран составляет 30,60, а точка касания оси струи экрана лежит за пределами расстояния «а», т.е. в области проема. При начальном угле истечения струи 00 в широком диапазоне расстояний (с/bз), начиная от 2,5, искривление струи также незначительно, точка касания с экраном располагается дальше, чем при угле 300.
Дадим оценку дополнительному разрежению, возникающему в пространстве между корпусом завесы и экраном. В этот промежуток устремляется расход воздуха, эжектируемого струей на длине экранирования «а» и равный Gэа = 0,5(λа – 1)Gз. Средняя скорость воздуха при тех же параметрах и при скорости на выходе из сопла завесы 12 м/с не превышает 1 м/с. Соответственно, возникает разрежение не более 0,5 Па.
Таким образом, можно пренебречь влиянием ограниченного пространства на формирование экранируемой струи и рассматривать ее, как свободную затопленную.
3. Введем обобщенный показатель действия завесы – параметр q как
q̃ = Ga/(Ga + Gн) (1)
где Ga – массовый расход струи на уровне верхней кромки проема (аналог расхода через завесу в принятой интерпретации показателя q для неэкранированных струй), Gн – массовый расход части наружного эжектированного на длине (h – a)/cosα воздуха, затекающего в проем. Уравнение импульсов в проекции на направление, перпендикулярное плоскости проема, позволяет выразить (1) в виде
q̃ = 2λa(v̅1 + v̅2)[2(σ - sinα) + v̅1(λh + λa) – v̅2(λh – λa)]-1 (2)
Здесь σ = ΔP̅прF̅̅, F̅= Hпр/bз, ΔP̅пр = ΔРпр/ρvз2, v̅1 и v̅2 – среднемассовые скорости потоков, растекающихся от проема наружу и вовнутрь, отнесенные к скорости струи в сопле vз , λh – коэффициент эжекции струи в сечении «h». Полагая, что скорости v̅1 и v̅2 по порядку величины не должны отличаться от среднемассовой скорости струи перед поворотом в проем v̅с, а также используя условие сохранения потока импульса вдоль струи до поворота, получим
v̅1 = v̅2 = v̅с = 1/λh (3)
Подставляя (3) в (2), найдем
q̃ = 2(λa/λh)(σ – sinα + λa/λh)-1 (4)
Струя развивается по законам свободной затопленной от сопла до области поворота внутрь помещения (см. рис.1).
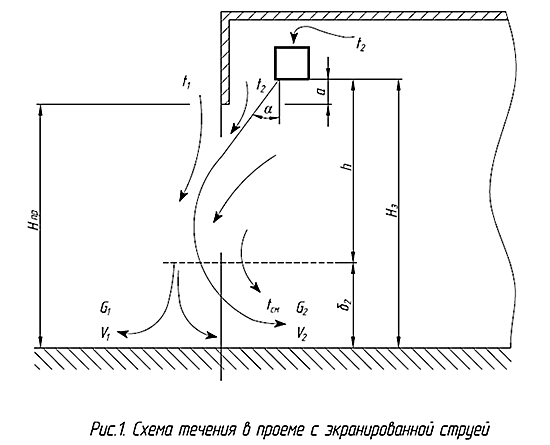
Расчетная длина струи определяется как z = h/cosα. Принято, что толщина струи, затекающей в проем, связана с h равенством
δ2 + h = Hз (5)
Развертывая и преобразовывая выражение (5), получим обобщенное на рассматриваемый случай уравнение для определения коэффициента эжекции
λh = (F̅+ a̅)0,5[cosα/(0,55/ξ)2 + 0,5(1 + σ – sinα)]-0,5 (6)
где a̅= a/bз .
Таким образом, при заданных величинах α, σ, a̅, F̅ можно вычислить коэффициенты эжекции λa и λh и далее параметр q̃ . При этом «традиционный» показатель действия завесы будет равен
q = [λa/ q̃ - 0,5(λa – 1)]-1 (7)
или, после подстановки q̃ по (4)
q = 2[1 + λh(σ – sinα)]-1 (8)
Устремляя a → 0, чисто математически получим λа→ 0. Однако физический смысл имеет только λ ≥ 1, чему соответствует некоторое минимальное конечное расстояние от сопла. Это является следствием упрощения действительной структуры струи, которое позволяет отсчитывать расстояние не от полюса струи, а от выходного сечения сопла. Если при а → 0 положить λа = 1, то выражение (4) превращается в (8), что и подтверждает тождественность физического смысла того и другого. Сравнивая (4) и (8), легко убедиться в том, что q ≤ q̃. При q̃ = 1 выражение (7) становится равным
q| q̃ =1 = 2/(λa + 1) (9)
и это означает, что струя с расходом Ga заворачивает в проем, а массы, эжектированные на участке между сечениями «а» и «h», отделяются и уходят на улицу.
При q = 1 вся наружная эжекция Gэh = 0,5(λh – 1)Gз, включая ее экранированную часть, отделяется от струи и уходит на улицу, а показатель равен
q̃|q=1= λa/[1 + 0,5(λa – 1)] (10)
По аналогии с неэкранированной структурой можно показать, что вся струя с расходом Gh = λhGз затекает в проем (предельный режим защиты) при
q̃*= 2λa/(λa + λh) (11)
Это минимальное значение показателя, при котором неэжектированный снаружи воздух не прорывается под струей. Используя полученные зависимости, найдем расход уходящей на улицу части струи. При q̃* ≤ q̃ ≤ 1
G1 = Gэh - Gэa– Gн = [0,5(λh – 1) – 0,5(λa -1) – λа(1/ q̃ – 1)]Gз (12)
Его доля в наружной эжекции составляет
η = 2[0,5(λh + λa) – λa/ q̃ ]( λh – 1)-1 (13)
Для иллюстрации полученных выражений рассмотрим проем, защищенный завесой со следующими параметрами: Нпр = 4 м, В = 4 м, bз = 0,15 м, а = 1 – 3 м, vз = 12 м/с, t1 = -300С, t2 = 180С, Gз = 31100 кг/час, ξ = 0,8, α = 300. Расчеты по выражениям (4) – (6) приведены в табл.1.
Таблица 1. Расчетные аэродинамические параметры экранированной завесы.
| Параметры | Высота экранирования «а», м | |||
| 0 | 1 | 2 | 3 | |
| λа | 1 | 1,92 | 2,70 | 3,32 |
| λh / q̃ при ΔPпр = 6 Па |
3,25 / 0,84 | 3,63 / 1,11 | 3,97 / 1,23 | 4,29 / 1,29 |
| λh / q̃ при ΔPпр = 7 Па |
3,2 / 0,70 | 3,58 / 0,96 | 3,92 / 1,09 | 4,23 / 1,15 |
| λh / q̃ при ΔPпр = 8 Па |
3,15 / 0,60 | 3,53 / 0,85 | 3,86 / 0,97 | 4,17 / 1,04 |
| λh / q̃ при ΔPпр = 10 Па |
3,07 / 0,48 | 3,45 / 0,70 | 3,75 / 0,82 | 4,06 / 0,88 |
Из табл.1 видно, что понятный значительно более интенсивный рост λа в сравнении с λh при увеличении степени экранирования приводит к повышению показателя q̃ в полном соответствии с выражением (4). Увеличение разности давления в проеме снижает уровень показателя q̃ и при 10 Па он становится равным предельному нижнему значению q̃* по (11).
4. Проанализируем теплопотери экранированной струи с отделяющимися и уходящими на улицу массами. С этой целью, в первую очередь, оценим интенсивность охлаждения ядра постоянного расхода. Подход к этому состоит в выделении ядра постоянного расхода струи и приложении к ядру методов теории теплообменных аппаратов с введением аналогов конвективных коэффициентов теплоотдачи [3]. Показано, что в свободной затопленной струе коэффициент теплоотдачи определяется из критериального выражения St = 0,065(L/bз)-0,444, где St = α/(ρCpvз) - критерий Стантона.
Рассмотрим тепловой поток от ядра постоянного расхода ненагретой струи в сторону улицы. В общем случае, от площадки dF ядра с наружной стороны струи уходит теплота
dQ = α(tя –t1)dF = (t2 – t1)Wяθdε (14)
Здесь α – коэффициент конвективной теплоотдачи от ядра постоянного расхода струи принимается постоянным средним на длине струи, Wя = GяCp – водяной эквивалент ядра постоянного расхода, параметр ε = αF/Wя называют числом единиц переноса теплоты. Безразмерная температура ядра постоянного расхода θ = (tя – t1)/(t2 – t1) формируется как уходом теплоты наружу, так и поступлением ее изнутри здания. В [3] найдено для неэкранированной струи
θx = 0,5[1 + exp(-2εx)] (15)
Важно, что из критериального выражения для числа Стантона непосредственно получается равенство ε = 0,065(L/bз)0,556 .
Подстановка (15) в (14) и интегрирование от x = 0 до L дает
Q̃|0L = 0,25[1 – exp(-2εL)] + 0,5εL (16)
Здесь Q̃|0L = Q|0L / (t2 – t1)Wя. Можно показать, что для экранированной холодной струи, у которой в промежутке от х = 0 до х = а теплопотери отсутствуют и температура всей струи в сечении «а» равна t2, выражения (15) и (16) преобразуются в
θx = 0,5[1 + exp(-2(εx – εа))] (17)
Q̃|0L = Q̃|aL = 0,25[1 – exp(-2(εL – εa)] + 0,5(εL - εa) (18)
Оценка теплопотерь по (18) до некоторой степени условна, поскольку предполагает, что температура всей эжектированной массы около ядра постоянного расхода не зависит от втекания эжектированных масс Gэа с температурой t2. Введем корректировку выражения (18), используя приближенную оценку условного повышения температуры t1 до t1усл. Рассчитаем среднюю температуру смешения tсм теплоты экранированной части эжекции Qэа = GэаСр(t2 – t1) с холодной наружной частью эжекции без учета прихода теплоты от ядра постоянного расхода. Условную температуру для расчета теплопотерь ядра примем равной t1усл= 0,5(t1+ tсм), а полную теплоту в потоке эжекции Qэh = Qэа + Q|aL (при t1усл). После соответствующих подстановок и преобразований получим окончательно
Q̃эh = Qэh / GзСр(t2 – t1) = 0,5(λа – 1) + Q̃|aL [1 – 0,5(λа – 1) / (λh – 1)] (19)
Потери с уходящими наружу массами равны
Q̅пот = ηQ̃эh (20)
5. В завершение дадим числовые оценки двум основным проектным параметрам: температуре смеси tсм, втекающей в защищенный экранированной струей проем, и тепловой мощности компенсации теплопотерь Qкомп = GсмCp(t2 – tсм), где Gсм – суммарный расход смеси, втекающей в помещение от защищенных ворот. Под компенсацией здесь понимается такая организация защиты проема, когда затекающий от ворот в помещение поток подогревается независимыми воздухоподогревателями и внутренняя температура поддерживается постоянной и равной t2. Величина этой тепловой мощности может служить мерой энергетической эффективности организации защиты. Реально в период открытых ворот во многих случаях допускается понижение температуры в помещении с последующим более или менее длительным ее повышением до заданной величины. В таких случаях тепловая мощность компенсации меньше введенной здесь Qкомп , хотя энергетические затраты на компенсацию могут оставаться неизменными.
Для экранированной струи при q̃ ≤ 1 тепловой баланс
(tсм – t1)(Ga + Gн + Gэhв – Gэaв) = = Ga(t2 – t1) + Gн(t1 – t1) + (Gэhв – Gэaв)(t2 – t1) - Q̅потGз(t2 – t1), (21)
в данном случае Gсм = Ga + Gн + Gэhв – Gэaв, верхним индексом «в» отмечены расходы эжекции внутренних масс.
После преобразований безразмерная температура смеси будет
θсм = (tсм – t1)/(t2 – t1) = [0,5(λh + λa) - Q̅пот][λa/q̃ + 0,5(λh – λa)]-1 (22)
Тепловой поток компенсации после подстановки (22) и преобразований равен
Q̅комп = λa(1/q̃ - 1) + Q̅пот (23)
Из (23) видно, что на режиме q̃ = 1 Q̅комп = Q̅пот, в остальных случаях необходима компенсация не только потерь с уходящими массами, но и втекающих холодных масс эжекции (q̃ < 1). На предельном режиме q̃ = q̃* Q̅пот = 0 и с учетом (11) Q̅комп = λa(1/q̃* – 1) = 0,5(λh – λa).
Для экранированной струи при q̃ > 1 в выражении теплового баланса (21) изменится сомножитель при слагаемом Gн. Вместо (t1 – t1) = 0 появится сомножитель (t2 – t1), поскольку этот поток приходит не снаружи в проем, а уходит изнутри (из Gа) с температурой t2 . Кроме того, величина Gн становится отрицательной и равной λa(1/q̃ – 1) Gз . Выражение (22) преобразуется в
θсм = [λa/q̃ + 0,5(λh – λa) - Q̅пот][λa/q̃ + 0,5(λh – λa)]-1 (24)
а выражение (20) остается неизменным вместе с (13).
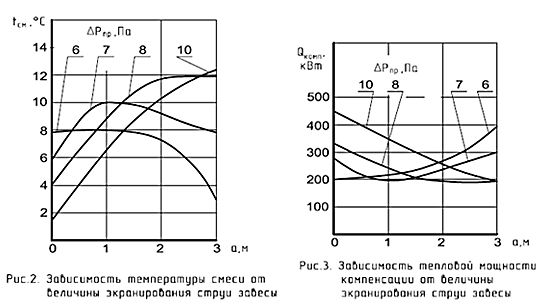
Результаты расчета основных параметров защиты проема экранированной струей приведены на рис.2 и 3 для условий примера из раздела 3. Теплопотери ядра постоянного расхода струи определялись по полной длине струй с учетом угла 300. Для интерпретации полученных результатов рис.2 и 3 необходимо рассматривать совместно с табл.1. На режимах работы q̃* ≤ q̃ ≤ 1 имеем очевидный результат: температура смеси tсм растет вместе с q̃ независимо от разности давлений на проеме и величины экранирования. Очевидность опирается, в первую очередь, на снижение доли поступающего в проем холодного наружного воздуха. Это обстоятельство начинает играть главную роль при q̃ → q̃* . Например, при ΔPпр = 10 Па, когда показатель q̃ = q̃*, его величина возрастает от 0,48 на режиме без экранирования до 0,88 в случае с максимальным экранированием, а температура смеси возрастает от 1,3 до 12,70С.
Для понимания феномена целесообразно рассмотреть предельный случай q̃* = 1, т. е. ситуацию совмещенных режимов полного затекания струи в проем и отсутствия проникновения в проем холодного наружного воздуха. Это становится возможно, если формирование струи до поворота закончилось за экраном в сечении «а» и с этого сечения начался поворот струи внутрь помещения. Из (11) следует, что при q̃* → 1 будет λh → λa и, соответственно, h → a. Приравнивая выражение (6) к λa , найдем для ΔPпр = 10 Па а¯*= 47,4 или а*= h* = 7,1 м. Нижним индексом «звездочка» здесь отмечена принадлежность размеров к предельному режиму q̃*. Поскольку на этом режиме Q̅пот = 0, то из (22) следует θсм = 1, т.е. tсм = t2.= 180С. При всей неожиданности подобного результата, он легко объясним в рамках принятой модели. Вся струя до сечения поворота сформирована из внутреннего воздуха с температурой t2. Начиная с сечения «а», которое совпадает с верхней кромкой проема, начинается поворот струи внутрь помещения. Принятая модель пренебрегает незначительной эжекцией наружных масс на участке поворота струи с их последующим отделением и уходом на улицу. Из этого и следует Q̅пот = 0. Для «нормальных» ситуаций, когда предельные режимы q̃* и q̃ = 1 достаточно удалены друг от друга, данное упрощение вполне справедливо. Однако в ситуациях сближения предельных режимов при экранировании струи, вплоть до их совпадения, пренебрежение потерями на участке поворота дает искаженный результат. Тем не менее, имеет место очевидная тенденция значительного повышения температуры смеси экранированием холодной верхней завесы в ситуациях, когда режим работы неэкранированной струи характеризуется показателем предельного режима q̃*.
На режимах работы с q̃ > 1 потери теплоты обусловлены не поступлением холодного наружного воздуха, а уходом части теплого воздуха из первоначального расхода на улицу. Температура смеси при этом падает с ростом показателя q̃. Наиболее выпукло это видно в случае ΔPпр = 6 Па.
Зависимости тепловой мощности компенсации на рис.3 имеют минимум. С возрастанием разности давлений на проеме минимум перемещается в сторону увеличения размера экранирования. В значительной степени положение минимума связано с максимумами температур смешения на рис.2.
6. Выводы.
Несмотря на принятые упрощения физической модели экранирования струи и некоторую идеализацию явления, выявлен значительный ресурс повышения эффективности защиты проемов холодными верхними завесами. Теоретически показано, что перемещая одну и ту же завесу вверх от кромки проема с учетом угла струи можно повысить температуру втекающей смеси на 1 – 100С в зависимости от разности давлений в проеме. При этом тепловая мощность компенсации может быть уменьшена в 1,3 – 2,0 раза по отношению к мощности без экранирования. Наиболее ярко эффект экранирования проявляется в ситуациях, когда режим работы неэкранированной завесы близок к предельному по полному затеканию сформировавшейся струи в проем.
Использованные источники
1. Ю.Н.Марр. Физическое моделирование защиты проемов завесами// Инженерные системы. АВОК-Северо-Запад. № 1. 2014.
2. Теория турбулентных струй. Издание 2-е переработанное и дополненное. Под редакцией Г.Н.Абрамовича. М.:Наука.1984.
3. Ю.Н.Марр. Теплообмен в струйных течениях// Инженерные системы. АВОК-Северо-Запад. № 3.2014.




